[高中数学人教版 A] 选择性必修第二册习题
Table of Contents
一元函数的导数及其应用
导数的运算
Question
- 已知函数 \(f(x) = \frac{x^2}{2} + 2x - 3\ln x\) ,求 \(f(x)\) 的导数,并求出 \(f'(x) > 0\) 的解集.
Solution
\(f'(x) = x + 2 - \frac{3}{x} = \frac{x^2+2x-3}{x}\). 要使 \(f'(x) > 0\) 有:
Case I, $ x > 0 \land x^2 + 2x - 3 > 0$, then \(x>1\).
Case II, $ x < 0 \land x^2 + 2x - 3 < 0$, then \(-3 < x < 0\).
综上,解集为 \((-3,0)\cup(3,+\infty)\). □
复习参考题
Question
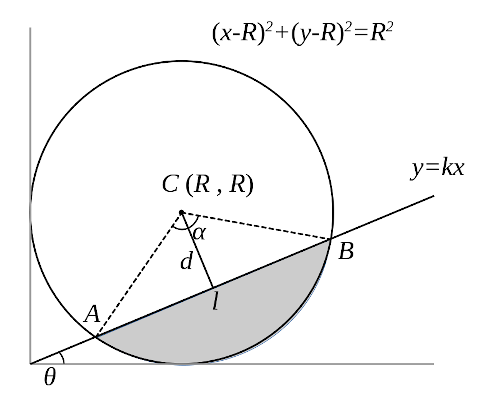
- 如图,直线 \(l\) 和圆 \(P\) ,当 \(l\) 从 \(l_0\) 开始在平面上按逆时针方向绕点 \(O\) 匀速转动(转动角度不超过 \(90\degree\) )时,它扫过的园内阴影部分的面积 \(S\) 使时间 \(t\) 的函数. 这个函数的图像大致是什么。
Solution 基本的考量是,取最开始的一个小 \(\d\theta\), 夹着的面积,是要小于线扫到中间的时夹着的面积,所以说,面积的增长应该是先慢,后快,再慢。
我尝试着推导一下,如下。
Let the equation of line be \(y=kx\), then the slope of the line is the tangent value of angle \(thete\).
\[ k = \tan\theta \]
The distance from point \(C\) to line is \(d\) by
\[ d(k) = \frac{k-1}{\sqrt{1+k^2}} R \]
Replaced \(k\), then
\begin{align*} d(\theta) &= \frac{ \tan\theta - 1 }{\sqrt{ 1 + \tan^2\theta}}R\\ &=\frac { \tan\theta - 1 }{\sec^2\theta}R\\ &=(\sin\theta - \cos\theta)R \end{align*}By Pythagorean theorem,
\begin{align*} l(\theta) &= \sqrt(R^2 - d^2(\theta))\\ &= \sqrt{\sin2\theta}R \end{ali□