[高中数学人教版 A] 选择性必修第三册习题
Table of Contents
计数原理:习题 6.1
Question 1.一个商店销售某种型号的电视机,其中本地的产品有 4 种,外地的产品有 7 种.要买 1 台这种型号的电视机,有多少种不同的选法?
Solution 要买 1 种,无其他限制条件,由分类加法原理: \(N=4+7=11\). □
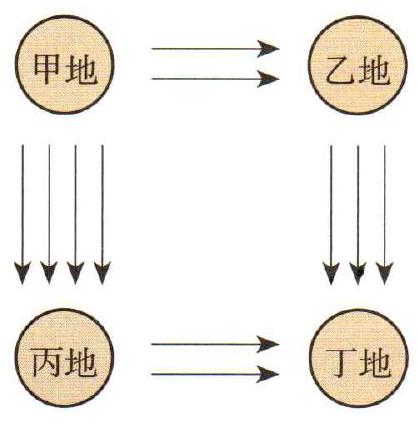
Solution 从甲到丁可分为两类:
- 从甲到乙,再到丁,由分步乘法原理: \(N_1 = 2\times3 = 6\).
- 从甲到秉,再到丁,由分步乘法原理: \(N_2 = 4\times2 = 8\).
最后由分类加法原理: \(N = N_1 + N_2 = 14\) □
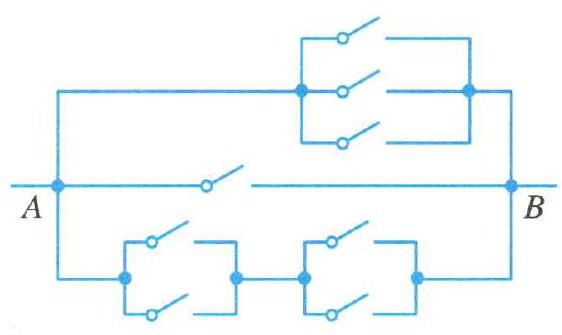
Solution A 接通 B 可分为三类:
- 上部接通,三选一皆可,由分类加法原理: \(N_1 = 3\)
- 中部接通,只有一种选择,故 \(N_2 = 1\)
- 下部接通,需要分步,而每步皆有两种选择,由分步乘法原理: \(N_3 = 2\times2 = 4\)
最后由分类加法原理: \(N=N_1+N_2+N_3 = 8\). □
Question 4.用 1,5,9,13 中的任意一个数作分子, 4,8,12,16 中任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?
Solution (1) 需要分别选取两个数,第一步有 4 中选法,第二步亦有 4 种,由分步乘法原理 \(N = 4\times4 = 16\). 1111 (2) 真分数需要分子大于分母。
| 分子 | 候选分母 | 种数 |
| 1 | 4,8,12,16 | 4 |
| 5 | 8,12,16 | 3 |
| 9 | 12,16 | 2 |
| 13 | 16 | 1 |
由分类加法原理, \(N= 4 + 3 + 2 + 1 = 10\) □
Question 5.一个口袋内装有 5 个小球,另一个口袋内装有 6 个小球,所有这些小球的颜色互不相同. 从两个袋子中分别取 1 个球,共有多少种不同的取法?
Solution 所有小球颜色互不相同,从第一个口袋取球有 5 种取法,而第二个口袋取球则有 6 种取法。由分步乘法原理, \(N = 5\times6 = 30\). □
Question 6.(1) 在平面直角坐标系内,横坐标与纵坐标均在 \(A=\{0,1,2,3,4,5\}\) 内取值的不同点共有多少个? (2) 在平面直角坐标系内,斜率在集合 \(B=\{1,3,5,7\}\) 内取值, \(y\) 轴上的截距在集合 \(C=\{2,4,6,8\}\) 内取值的不同直线共有多少条?
Solution (1) 这些数组成的坐标点都不会出现重复的情况,因此 \(N=6\times6\).
(2) 同上,斜率和截距的不同组合得到的直线也不会相同,因此 \(N=4\times4=16\). □
Question 7.一种号码锁有 4 个拨号盘,每个拨号盘上有 0-9 共 10 个数字. 现最后一个拨号盘出现了故障,只能在 0-5 这 6 个数字中拨号,这 4 个拨号盘可组成多少个四位数字号码?
Solution 拨号盘密码不要求第一位数非零,因此前三个位都可以取 10 个。又因最后只能取 6 个数字,故 \(N=10\times10\times10\times10\times6=6000\). □
Question 8.(1) 4 名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是 \(3^4\) 还是 \(4^3\) ? (2) 3 个班分别从 5 个景点中选择一处游览,不同选法的种数是 \(3^5\) 还是 \(5^3\) ?
Solution (1) 对于每位同学,都有 3 种球队可以选择报名参加,因此 \(N=3\times3\times\times3\times3=3^4\).
(2) 对于每个班级,都有 5 处风景可供选择,因此 \(N=5\times5\times5=5^3\). □
Question (1) 从 5 件不同的礼物中选出 4 件送给 4 位同学,每人一件,有多少种不同的送法? (2) 有 5 个编了号的抽屉,要放进 3 本不同的书,不同的放法有多少种?(一个抽屉可放多本书)
Solution (1) 对于第一个同学有 5 件礼物可选,第二个同学有 4 件,因此每人一件的总方案共有 \(N=5\times4\times3\times2 = 120\).
(2) 每本书可以选择 5 个抽屉存放,而一个抽屉可以放多本,因此 \(N=5\times5\times5=125\). □
Question 10.口袋中装有8个白球和10个红球,每个球编有不同的号码,现从中取出2个球. (1) 正好是白球、红球各一个的取法有多少种? (2) 正好是两个白球的取法有多少种? (3) 至少有一个白球的取法有多少种? (4) 两球的颜色相同的取法有多少种?
Solution (1) 只需要把球拿出来,故先拿白球和先拿红球无差别,总数 \(N_1 = 8\times 10=80\).
(2) 两个白球,因而各个球都由编号,如果直接 \(8\times7\) 会出现重复,比如说分别取到 1 号和 2 号的白球,和分别取到 2 号和 1 号的白球是等价的方案。
对于 1 号白球,第二个球有 7 种选择;对于 2 号白球,不能再取 1 号,所以只有 6 种选择。以此类推,第二个可选白球的数目随着第一个白球号数的增加而减少,因此种数应该是 \(N_2 = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28\).
(3) “至少有一个白球”,因此是“两个都是白球”和“恰有一个白球”的并集,因此 \(N_3 = N_1 + N_2 = 108\).
(4) 可用同 (2) 的方法计算出恰是 2 个红球的种数是 \(N'=\sum_{i=1}^9i = 45\),因此两球颜色相同的种数为 \(N_4 = N_2 + N' = 73\). □
Question 11.在国庆长假期间,要从 7 人中选若干人在 7 天假期值班(每天只需 1 人值班),不出现同一人连续值班 2 天,有多少种可能的安排方法?
Solution 除了第一天有 7 人可选,之后每一天的工人都不能与前一天相同,即有 6 人可选。总数为 \(N=7\times6^6=326592\). □
Question 12.2160有多少个不同的正因数?
Solution 首先对 2160 进行质因数分解,得 \(2160=2\times2\times2\times2\times3\times3\times3\times5\). 而它的正因数,是由这些质因数选择并相乘而得。
设其通式为 \(2^i3^j5^k\), 其中 \(i\in\{0,1,2,3,4\}, j\in\{0,1,2,3\}, k\in{0,1}\). 因此组成因数共有 \(N = |i|\times|j|\times|k| = 5\times4\times2 = 40\). □